Memphis Depay, Graziano Pelle en Alfred Finnbogason. Drie getalenteerde aanvallers uit de Eredivisie. Afgezien van hun positie, hebben ze echter nog een overeenkomst: ze bevinden zich op de bovenste drie posities in het schotenklassement, een lijst die bijhoudt hoe vaak iedere speler in een wedstrijd schiet. Memphis Depay voert de ranglijst aan met 4,9 schoten per duel, terwijl Pelle (4,2) en Finnbogason (4,0) het met de posities twee en drie moeten doen. Uiteraard is het fijn om spelers in je team te hebben met een goed schot, want: hoe vaker je op goal schiet, hoe groter de kans is dat je scoort en hoe groter de kans is dat je een duel wint. Maar hoe groot is deze kans? Is het mogelijk om, aan de hand van een schotverhouding, te bepalen hoe groot de kans is dat je een duel wint? En hoeveel procent kans is er op een gelijkspel?
Als data zijn alle Eredivisiewedstrijden van speelronde 1 tot en met speelronde 26 gebruikt.
Algemene data
In de 234 duels die dit seizoen gespeeld zijn, zijn 171 overwinningen geboekt. Dat houdt dus in dat in totaal 73% van alle Eredivisieduels wordt gewonnen. Om de juiste verhouding te bepalen tussen de eigen schoten en de schoten van de tegenstander, is gekeken naar het TSR (Total Shot Ratio). Deze verhouding deelt het aantal schoten dat je zelf gelost hebt, door het aantal schoten dat er totaal gelost is in een duel. Wanneer team A dus twee maal schiet en team B achttien maal, heeft team A een TSR van 0,100 (2/20) en team B van 0,900 (18/20). Wanneer we al deze TSR’s in groepen van 0,05 zouden indelen, valt meteen op dat het aantal gewonnen duels toeneemt naarmate het TSR groter wordt. Een logische situatie, aangezien: vaker schieten, is vaker scoren, is vaker winnen. In de onderstaande tabel is het aantal duels en het aantal zeges te zien waarin een team een TSR had dat in die bepaalde groep hoort.
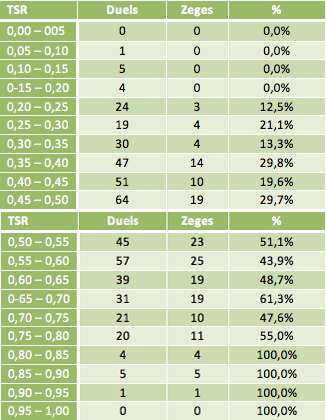
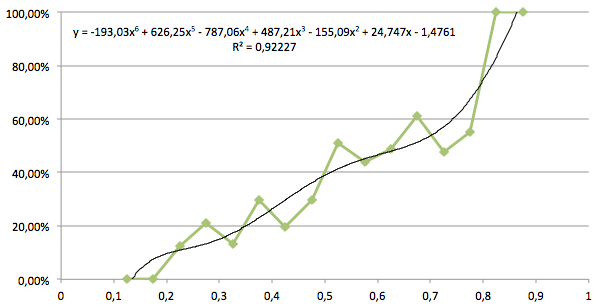
Bovenstaande grafiek geeft de percentages uit de tabel overzichtelijk weer. Wat opvalt, is dat de stijgende lijn een harmonisch verloop heeft: na een stijging komt er een kleine daling, die gevolgd wordt door één of twee stijgingen. We kunnen dus concluderen dat, gemiddeld genomen, de winstkans stijgt wanneer het TSR toeneemt. De zwarte lijn die door de grafiek is getrokken, heet de trendlijn. Een trendlijn is een functie (lineair, polynomisch of exponentieel) die het beste bij de opgegeven meetpunten past. Hoe goed hij er bij past, wordt bepaald door de R²: hoe dichter deze bij de 1 ligt, hoe beter de trendlijn bij de grafiek past. In dit geval is de R² gelijk aan 0,9223, wat inhoudt dat de trendlijn voor 92,23% bij de grafiek past. De trendlijn y is gelijk aan de volgende functie:
![]()
Hierbij stelt de winstkans voor (decimaal getal) en het TSR wat een team had (ook een decimaal getal). Hier moet wel een kanttekening bij worden gemaakt: de formule mag alleen gebruikt worden, wanneer het TSR van een team tussen 0,150 en 0,850 ligt. Hoe de verwachte TSR’s bepaald kunnen worden, komt verderop in het artikel ter sprake.
Kans op gelijkspel
Natuurlijk is er niet alleen een kans dat team A wint, of dat team B wint. Het is ook mogelijk dat een duel geen winnaar krijgt. In totaal zijn dit Eredivisieseizoen 171 van de 234 duels winnend afgesloten, wat dus inhoudt dat er 63 duels waren die geen winnaar kenden. Dit komt neer op 26,92% van de gevallen. De kans dat een wedstrijd in een gelijkspel eindigt, is uiteraard niet voor ieder duel gelijk. Zo is de kans dat Ajax – PSV gelijk eindigt groter dan de kans dat Ajax – Roda JC zonder winnaar wordt afgesloten, omdat Ajax tegen PSV minder vaak in schotpositie zal komen dan tegen Roda JC. Logischerwijs kunnen we dus zeggen dat de kans op een gelijkspel toeneemt, naarmate het TSR van beide teams dichter bij elkaar ligt. De kans dat een duel gelijk eindigt, berekenen we met de volgende formule:
![]()
Anders gezegd: de kans dat een duel gelijk eindigt, is 1 – het verschil in winstkans op basis van TSR tussen A en B, vermenigvuldigd met 63/234.
Hoe worden de TSR’s bepaald?
Zoals beschreven, schieten teams verschillende keren per duel op goal. Het ene team schiet echter vaker op goal dan het andere, en daarnaast maakt het ook verschil of een team thuis of uit speelt. Laten we twee situaties onderscheiden: een thuisduel en een uitduel. Voor de meeste teams is het logisch dat er in thuisduels meer op goal wordt geschoten dan in een uitduel. In onderstaande tabel is per team het gemiddelde aantal schoten in een thuis- of uitduel te zien.
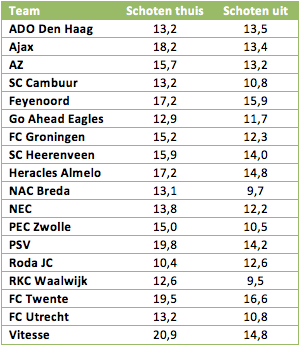
Wat opvalt in de tabel, is het lage aantal schoten in uitduels van Ajax: de Amsterdammers schoten per uitduel gemiddeld 13,4 keer op goal, minder dan teams als SC Heerenveen, Heracles Almelo en zelfs ADO Den Haag. Natuurlijk schiet een team niet ieder duel het gemiddelde aantal keren op goal, hier zit altijd een afwijking naar boven of naar beneden in. Per duel moeten de getallen dus gecorrigeerd worden, en dat wordt gedaan door de wortel te nemen van het aantal behaalde punten van de tegenstander in een bepaalde situatie (thuis of uit dus). Een voorbeeld: 
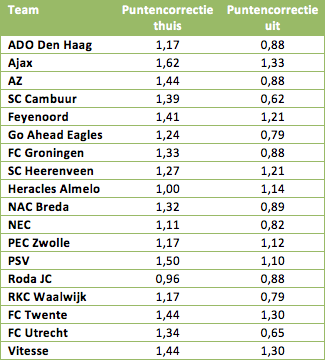
en uitduels
Is het mogelijk om de winnaar van een duel te voorspellen?
Ondanks dat er in een voetbalwedstrijd rekening gehouden met verschillende aspecten (derby’s, rode kaarten, schorsingen etc.) denken we dat het wel degelijk mogelijk is een voorspelling te maken van de winnaar. Wanneer de winstkans van beide teams bepaald is en de kans dat een duel gelijk eindigt bekend is, is het nog een kwestie van zorgen dat de som op 1 uitkomt. Een duel wordt namelijk door óf team A, óf team B, óf niet gewonnen. Het is nu natuurlijk erg verleidelijk om de winnaars van de komende Eredivisieduels te voorspellen.
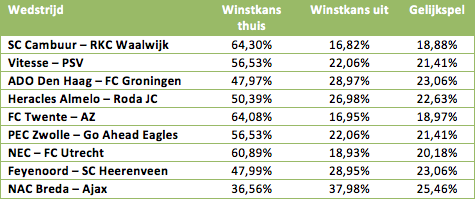
In de bovenstaande tabel zijn de winstkansen per team te zien in hun volgende duel. Vitesse is favoriet in de topper tegen PSV, met een winstkans van 56,53%. De kans dat PSV wint is 22,06%, terwijl er ook een kans van 21,41% is dat het duel gelijk eindigt. Ajax wint met een kleine 38% zekerheid van NAC, dat op basis van schoten en punten wel degelijk kans maakt tegen Ajax!



































Er zijn reacties op dit artikel
Laat reacties zien Hide commentsBeste Rick,
Erg interessant artikel en model!
Ik vroeg me af hoe je bij de formule voor de factorisatie komt, dat staat volgens mij niet beschreven in je artikel? Ik vroeg me ook af waarom je daar gemiddeld aantal punten gebruikt en niet bijv. schoten tegen? Zeker aangezien je denk ik in eerste plaats in dit soort modellen al schoten gebruikt omdat die een betrouwbaarder beeld geven dan punten.
Groet,
Mark
Beste Mark,
allereerst, dank voor je reactie. De formule waar ik toe ben gekomen, is gebruikt om het aantal schoten tegen een bepaalde tegenstander te bepalen. Sommige teams pakken heel weinig punten in uitduels, terwijl ze redelijk vaak schieten. ADO hiervan is een uitstekend voorbeeld, die schieten vaker in uitduels dan Ajax. Ik had inderdaad ook het aantal schoten tegen kunnen gebruiken, maar ook dan doe je tekort aan de kans dat een team wint: veel schoten tegen betekent namelijk niet automatisch een nederlaag. Als je naar de punten kijkt, krijg je in mijn ogen een mooi beeld van de sterkte van een team in een type duel (uit of thuis), dus vandaar dat ik daarvoor heb gekozen.
Met vriendelijke groet,
Rick
Ipv de wortel nemen professional gamblers de ‘league average’.
Dus: team A schoten voor + team B schoten tegen – league average schoten per team per wedstrijd.
Dat kun je onderverdelen in uit en thuis en/of in laatste vier wedstrijden (voor recente vorm) etc.
Daarna kun kijken naar quality shots. Doelpunten per schoten geeft daar wel een kijk op, maar de afstand en hoek op het doel spelen zeker mee. In ijshockey zie je bijvoorbeeld dat een verdediging de tegenstander naar de buitenkant van het ijs probeert te duwen, omdat vandaar de schoten veel minder gevaarlijk zijn.
Leuk artikel. Good luck!